1 Answer
Sounds like a rough Science Fair exhibit. Way over MY head, but I'm not really tall. The following is from WIKIPEDIA:
A compound pendulum (or physical pendulum) is one where the rod is not massless, and may have extended size; that is, an arbitrarily shaped rigid body swinging by a pivot. In this case the pendulum's period depends on its moment of inertia I around the pivot point.
The equation of torque gives:
<dl><dd>
 </dd></dl>
</dd></dl>where:
<dl><dd>
 is the angular acceleration.</dd><dd>
is the angular acceleration.</dd><dd> is the torque</dd></dl>
is the torque</dd></dl>The torque is generated by gravity so:
<dl><dd>
 </dd></dl>
</dd></dl>where:
<dl><dd>L is the distance from the pivot to the center of mass of the pendulum</dd><dd>θ is the angle from the vertical</dd></dl>
Hence, under the small-angle approximation 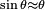 ,
,
<dl><dd>
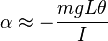 </dd></dl>
</dd></dl>This is of the same form as the conventional simple pendulum and this gives a period of:
<dl><dd>
 </dd></dl>
</dd></dl>And a frequency of:
<dl><dd>
 </dd></dl>
</dd></dl>Physical interpretation of the imaginary period
The Jacobian elliptic function that expresses the position of a pendulum as a function of time is a doubly periodic function with a real period and an imaginary period. The real period is of course the time it takes the pendulum to go through one full cycle. Paul Appell pointed out a physical interpretation of the imaginary period:[4] if θ0 is the maximum angle of one pendulum and 180° − θ0is the maximum angle of another, then the real period of each is the magnitude of the imaginary period of the other. This interpretation, involving dual forces in opposite directions, might be further clarified and generalized to other classical problems in mechanics with dual solutions
| 11 years ago. Rating: 1 | |

 deadsilence
deadsilence
 Bob/PKB
Bob/PKB






